モールス信号解析実験(FFT編)
40年ぶりに807とご対面しました。懐かしい! 10個500円という球のセットが有ったり、 動くのか動かないのか分からん(売ってる人も分からんと言っていた)軍用無線機とか 丸型ブラウン管タイプのオシロがあったり、もう、カオスですよ。こういうノリ好きだなあ。
1955年発行のCQ誌を展示してるブースが有ったので、古典を紐解いてみました。アンテナの 利得を計算する式を解説してたり、AGCのアタックタイムはどう設定するのが良いかなんて のを数ページ使って解説してたり、濃い話満載。こういうのに触れながら、電波少年は大人に なったのね。
自作品コンテストの表彰式があったので、謹んで参加してみました。受賞者のほとんどは、 もう初老(失礼)の方ばかり。若い人がさっぱり居なかったのは、一抹の不安がありました。 会場をうろうろしてる人も、お年寄りばかり、若い人を見つけるのは難しいぐらい。 出展クラブで、XXX大学無線クラブに若い人を見ただけ。
メーカーのブースでは、車が一台買えるぐらいなマシンにご対面。つまみがいっぱい。液晶 パネル付きが当たり前。DSPを豪華に何個も積んでいたりでびっくり。電源入れても、数分は 音が出ない受信機って? 球の受信機でもそんなに遅くはなかったよ。
しつこく聞いてみたら、Linuxを搭載してるとか。boot時にペンギンさんは見れなかったけど 確かにLinuxが起動してました。気が向けばWindowsも動かせるそうです。
波形を眺めてみて...
前回録音したモールス信号を、Media Playerで聴いてみた。くぐもりも感じられすに 綺麗に聞こえたよ。短点スピードが50msのやつは、残念ながら全く取れない。 CWの世界では、モールス信号のスピードを、WPM で表現するようだけど、50msのやつは 何WPMになるのだろう? ハムフェアで聞いてくれば良かったな。
「百聞は一見にしかず」と言うから、今度は波形を眺めてみる。我が家には、オシロスコープ 兼スペクトラムアナライザー兼声紋分析器である 「サウンドモニター FFT Wave」がある。 残念ながらシェアウェアで、試用期間が過ぎてしまうと、録音が出来なくなってしまうけど、 私みたいな用途には重宝する。
ちゃんと金払って、正規ユーザーになれよと言われそうだが、送金手続きが面倒なのでほってある。 郵便切手同封とかでもいいなら、使うに恥ずかしい(ミッキーの切手とか)やつがあるんで、送り ますよ。
波形を眺めてみると、440Hzと800Hzで全く、波形振幅が違う事に気づいた。440Hzの方は振幅が 小さいのである。6dB ぐらいは小さいかな。もっとかな? なぜだ? 980円のヘッドセット じゃ、フラットなf特を期待するのは、無理ってもんですと、マイクに凝っているCQ誌連載の あの方に、お叱りを受けそうである。
波形は、2f、3fの高調波が含まれているのは、お約束事項という事で、改めて確認した次第。 綺麗な正弦波を望むなら、DDSかな。
FFTどうしよう?
Unix系で使うなら、GNUが出している GSL (GNUサイエンスライブラリー)を取ってくれば たいがいの事は出来る。勿論、このライブラリーの中には、FFTもWavelet変換も含まれている。 この膨大なライブラリーを翻訳して公開 されているので、眼を通しておくと、良いだろう。
また、「餅は餅屋」と言うならば、FFT専門のライブラリーも提供されてる。 FFTWがそれだ。旧版のfftwとfftw3があるが、今から使うなら fftw3系がいいだろう。
FreeBSDでは、gsl、fftw3も含めて、port/mathにあるので、入れておくといいかも。
今回は、fftをやりたいので、fftw3かなと思って使い方を調べてみた。 計画を立ててから使うのね。SQLの実行戦略解析みたいで、ちと、おいらの趣味に合わない。(な んと贅沢な!)
結局、JA3CLMさんが参考にされたという、虎戯 から写経したのがあったので、それを使う事に した。(実験の残骸物ですから、ちと記事と違うかも知れません。Bugってても、著者の方を 攻めないでください。)
FFTのスピードは?
実行スピードの期待値は、もろもろのものを勘案して、2ms以内かなあと、推定した。 まずは、256ポイントのfftがどのくらいのスピードで実行出来るか、測ってみる。 ちと、ソースは長くなるけど、全掲載する。
// FFT sample from CQ/TR 2006.08
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <fcntl.h>
#include <sys/time.h> // for timming meas
#define INfile "sound.au"
#define DATAN 256
double WaveL[DATAN]; // tW input wave
double SpecL[DATAN]; // fA output spectoram abs
double cmpXL[DATAN]; // fR output spectoram real part
double cmpYL[DATAN]; // fI output spectoram image part
void fft(double *tW, double *fA, double *fR, double *fI) {
int N = DATAN;
int N_2 = N/2;
int i,j,k,kp,m,h,P;
double mdd;
double w1, w2;
double t1,t2,s1,s2;
double tri[DATAN];
double fReal[DATAN], fImag[DATAN];
// Get P, where N = 2 ** P
i = N; P = 0;
while (i != 1) {
i = i / 2;
P++;
}
// copy real wave into buffer
for (i = 0; i < N; i++) {
fReal[i] = tW[i]; fImag[i] = 0.0;
}
// make sin,cos table
for ( i = 0; i < N_2; i++ ) {
tri[i] = cos( 2 * i * M_PI / N );
tri[i + N_2] = (-1.0) * sin( 2 * i * M_PI / N );
}
// sort
j = 0;
for ( i = 0; i <= N - 2; i++ ) {
if (i < j) {
t1 = fReal[j]; fReal[j] = fReal[i]; fReal[i] = t1;
t2 = fImag[j]; fImag[j] = fImag[i]; fImag[i] = t2;
}
k = N_2;
while (k <= j) {
j = j - k; k = k/2;
}
j = j + k;
}
// do butterfly
for ( i = 1; i <= P; i++ ) {
mdd = pow(2.0, (double)i);
m = (int)mdd;
h = m/2;
for ( j = 0; j < h; j++ ) {
w1 = tri[j*(N/m)];
w2 = tri[j*(N/m) + N_2];
for( k = j; k < N; k+=m ) {
kp = k + h;
s1 = fReal[kp] * w1 - fImag[kp] * w2;
s2 = fReal[kp] * w2 + fImag[kp] * w1;
t1 = fReal[k] + s1; fReal[kp] = fReal[k] - s1; fReal[k] = t1;
t2 = fImag[k] + s2; fImag[kp] = fImag[k] - s2; fImag[k] = t2;
}
}
}
// fft result copy for output
for ( i = 0; i < N; i++ ) {
fA[i] = sqrt(fReal[i] * fReal[i] + fImag[i] * fImag[i])/DATAN;
fR[i] = fReal[i];
fI[i] = fImag[i];
}
}
winfunc( double *tW, char *type){
int i;
int N = DATAN;
if ( strcmp( type, "han") == 0 ){
for ( i = 0; i < DATAN; i++ ){
tW[i] *= 0.5 * (1.0 - cos(M_PI * 2 * i / (N - 1)));
}
}
if ( strcmp( type, "black-h") == 0 ){ // Good for amp reolution
double a0 = 0.35875;
double a1 = 0.48829;
double a2 = 0.14128;
double a3 = 0.01168;
double k;
for ( i = 0; i < DATAN; i++ ){
k = a0 - a1 * cos(M_PI * 2 * (i + 0.5) / N)
+ a2 * cos(M_PI * 2 * 2.0 * (i + 0.5) / N )
- a3 * cos(M_PI * 2 * 3.0 * (i + 0.5) / N );
tW[i] *= k;
}
}
}
disp(double *fA, double *fR, double *fI){
int i;
for ( i = 0; i < DATAN / 2; i++ ){
printf("%6d %10.1f \n", i, fA[i] );
}
}
load_wave(double *tW){
int i;
signed short buf[DATAN];
FILE *fp;
fp = fopen(INfile, "rb");
fread(&buf, sizeof(signed short), DATAN, fp);
fclose(fp);
for (i = 0; i < DATAN; i++){
tW[i] = (double)buf[i];
}
}
main(){
struct timeval st,sp;
gettimeofday(&st, NULL);
load_wave(WaveL);
winfunc(WaveL, "black-h"); // "none" : Good for freq resolution
fft(WaveL, SpecL, cmpXL, cmpYL);
gettimeofday(&sp, NULL);
disp(SpecL, cmpXL, cmpYL);
printf("%dus\n", (sp.tv_sec - st.tv_sec) * 1000000 + (sp.tv_usec - st.tv_usec) );
exit(0);
}
コンパイルは
[sakae@fb ~/CW]$ cc -g -lm -o a.out myfft.c
実行結果は
[sakae@fb ~/CW]$ ./a.out
0 16.5
1 19.0
2 53.7
3 50.4
4 30.7
5 8.9
6 6.6
7 7.7
8 1.2
9 5.1
10 1.2
11 18.2
12 124.1
13 434.4
14 673.8
15 484.6
16 141.9
17 2.9
18 5.6
.....
125 12.7
126 36.2
127 39.0
871us
データを読み込んで、窓関数による補正を加えてからFFTしてる訳だが、それに要する時間は 大体900usか。まあまあだな。参考までに、512ポイントでは、1.4ms 1024ポイントのFFTでは、 2.3msだった。この結果からすると、512ポイント以下がリミットかな。
モールス波形抽出もどき
先の実験は、録音データの一番最初の部分のみを対象にスピードを評価した訳であるが、 全体を通して実行したら、どんな風になるだろう? どうせやるなら、注目波形(440Hz,800Hz)近傍のみを抽出する事にする。そのため、上記の プログラムをちと改造する。
main(){
int cnt = 122880 / DATAN; // 122880 =~ # of samples @ 8000/sec * 15sec
FILE *fp;
double s4,s8;
int d4,d8;
double th = 1000.0; // thereshold for 1/0
fp = fopen(INfile, "rb");
while(cnt--){
load_wave(WaveL, fp);
winfunc(WaveL, "black-h"); // "none" : Good for freq resolution
fft(WaveL, SpecL, cmpXL, cmpYL);
s4 = SpecL[13] + SpecL[14] + SpecL[15]; // 440Hz
s8 = SpecL[26] + SpecL[27] + SpecL[28]; // 800Hz
d4 = s4 > th ? 1 : 0;
d8 = s8 > th ? 1 : 0;
printf("%10.1f %10.1f %d %d\n", s4, s8, d4, d8);
}
fclose(fp);
exit(0);
}
録音波形を256ポイント毎にFFTし、440Hz,800Hzの振幅成分を抽出しようと言う訳である。 モールス波形のスペース部分は、当然440Hzの音成分は無いから、理想的には零に なるはずである。この閾値として、1000を選んだ。
[sakae@fb ~/CW]$ ./a.out
1592.8 7.7 1 0
1683.2 20.8 1 0
1724.9 16.9 1 0
258.0 41.6 0 0
107.6 14.0 0 0
16.5 14.2 0 0
1514.6 30.2 1 0
1682.6 7.4 1 0
1738.4 8.2 1 0
.....
17.1 51.5 0 0
14.0 31.6 0 0
25.0 28.5 0 0
20.3 12.8 0 0
左から、440Hzの振幅、800Hzの振幅、その右側には、それぞれを2値にしたものが表示されて いる。 これをグラフにすると
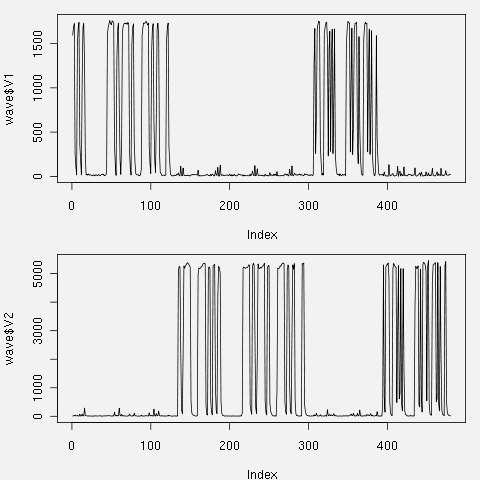
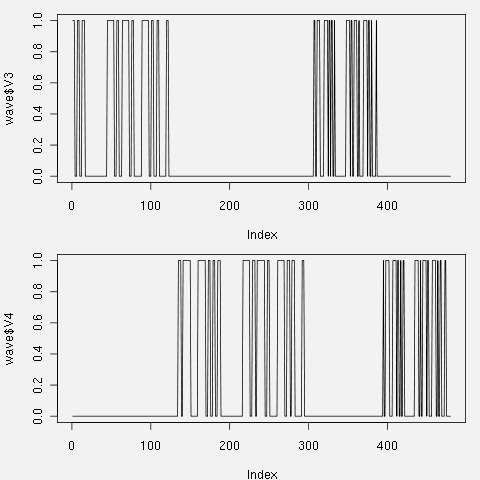
これを見ると、短点スピードが50msでは、波形の抽出が怪しい。そもそも、何も考えずに 256ポイントでFFT、元信号は、8000回/秒のサンプリングであるから、1回のFFTでは、 32ms(= 256/8000)の区間を調べてる事になる。32ms対50msと言う事で、タイミングが ずれたりすると、正しく認識できなくなるのだ。(JA3CLMも、この点で、非常に苦労されてます)
さて、おしまいに、15秒のデータをFFTするのにどのくらい時間がかかったか、調べておく。
[sakae@fb ~/CW]$ time ./a.out > /dev/null real 0m0.228s user 0m0.225s sys 0m0.001s
480回FFTを行って、この時間だ。1回に直すと、470us。上の実験と大差が でた。何故?